Design Of Steel Beam Fastest Method With Example

Design Of Steel Beam Fastest Method With Example

by | Sep 27, 2014 | Steel Design

Civil Engineering is vast field from Culverts to Dam , Buildings To Steel Bridges, so as so the Civil Engineering Materials, It includes Steel, Concrete, Timber, Aluminium, Glass etc. Steel Design is much easier in most of the cases than RCC Design in Structural Engineering. Civil Engineering Broadly has three main phase namely Planning – consisting of Drawing, Estimating etc. Structural Engineering Design consisting of Analysis of Structures and Design Of Structures and last of all Execution which means erecting the actual work according to the Planning and Designing. Structural Engineering has always been a field of respect amongst all the Civil Engineers. Today I will discuss about a part of Structural Engineering which will be dedicated toward the Design of Steel Beam specifically Steel I Beam. After reading this article you will be able to design a steel beam by your own without any problem. To make the explanation easy for understanding I will elaborate a simple yet considerably good problem which will cover all your needs as far as the Civil Engineering and Structural Design is concerned. I know now a days all the Structural Engineering Analysis and Design is being done by Computer Software like STAAD Pro, Ansys and all that, but without having the knowledge of manual Design of civil and structural engineering all those are useless because you will be not able to understand the Design Data and the outcome from the software.
But before going to start You need to understand few things which I should tell you first or at the later stage you may find some problem.

 

What is a Structural Engineer and Job Profile :- 

Civil Engineering as you already know is a vast field with full of opportunities, there are every aspect of civilization which is either directly or indirectly elated and proportional with the growth of the civil engineering field itself. Civil Engineering mainly deals with the few categories of engineers who take cares of different things, like Structural Engineer who deals with the all civil engineering structural design and analysis works for the safety and stability of the structure. Another important filed very close to Structural Engineering is Geotechnical Engineering which deals with the all about soil and its data collections tests bearing capacity determinations etc. And there is also Construction Engineers who do the actual construction on the field. In civil engineering structural engineer generally performs the structural design of Beams columns foundations slabs and other structural components, and also does the analysis jobs of an existing structure for determining its ability to carry loafs that it has been designed for. These Structural Engineer are well recognized among all the other fields of civil engineering. Structural Engineer and there jobs are mainly outsourced to a third party structural engineering firms in most cases.

As a Civil Construction material steel was vastly used in early days for building works and in cases where the loads are heavy but now a days most of the buildings are made of RCC however Steel is used in the places like Steel Bridge Design, Railways, Docks , Over bridges and etc. places where the loads are very heavy because the Bearing and Shearing capabilities of Steel is more than Concrete. And many a buildings in places like United Kingdom, United States, Australia and many other modern countries Slab Beam and Column Design are still being done with Steel as a Civil Construction material. Steel which are used in structural design as a construction material are used in the form of Rolled Steel Sections of different shapes like I Sections, Channels, Tubes, and also in built up sections. For Design of Steel beam mainly I sections are used. Now remember that great equation of the Theory of Bending which is (M/I) = (f/y) = (E/R) , I know you can steel recall this don’t you?. Okay let us just recap it in an easy way, in this equation the denotations are as follows :-

M = Bending Moment Acting on the Beam due to loads
I = Moment of Inertia of the Beam section
f = Bending Stress in the Steel Beam
y = Distance between the any fibre of section and the Neutral Axis [For getting maximum Bending Stress the value of y must be maximum as the Bending Stress is directly proportional to the distance between fibre at a point and the Neutral Axis, hence we need to consider extreme fibre which gives maximum value of ‘y’, this equals to h/2 where h is the depth of section, as the Neutral Axis of symmetrical sections like I-Section will fall at its C.G.]
E = Modulus of Elasticity of the Beam section
R = Radius of Curvature of the Shape of Bending of the Beam
 
But we won’t be needing all these, we just need the (M/I) =(f/y) for the design of steel beam.
Now we can rewrite the equation (M/I) =(f/y)  as (M/f) = (i/y) can we? Yes we surely can by cross multiplication. Here the term obtained (i/y) is known as Section Modulus and this is a very important factor because upon it the strength of any section depends. Actually When the Maximum distance between Neutral Axis and the fibre is considered, that is the distance between the Neutral Axis and the extreme fibre, meaning the maximum value of ‘y’, This term (i/ymax) or Section Modulus is denoted with ‘Z’ , therefore Z=(i/ymax) . I hope up to this level you have understood, and these things you have already studied in structural analysis isn’t it? Yes you have for sure. So basically in a Structural Steel Design of Beam we will design the beam for flexur, that is for Maximum Bending Moment and then chose a suitable Beam section from the list of available sections which varies from country to country and this list can obtained from bureau of standards of your country. And after choosing that section then we will check for other factors like Shear Stress, Deflection and look if that section can stand safely. That’s all isn’t it simple? Okay now lets get started, I will discuss How to Design a Steel Beam in Step By Step that You cannot escape without Understanding.
Let us consider a problem for explanation, suppose there is a hall room measuring 15m X 6m inside and the walls are 250mm thick. And it is given or you have thought to provide beams at a centre to centre distance of 3m apart. The beams are supporting a R.C.C. roof slab of 150mm thick with finishing on it, the flanges being restrained on slab. The Hall is a commercial type building. So let us design these beams.

 

Step 1 – Preparing a Neat Sketch from the Problem For Steel Beam Design :-

This is important in all types of Civil Engineering Structural Design Problem. As You know Drawing is the Language of Engineers and Line is the Language of Drawing, so prepare a neat drawing after reading the problem and give all the dimensions possible in the drawing. A Drawing is a must and it must be 100% correct as all the designing will be dependent upon this drawing. So prepare the drawing with caution. Here I’ve prepared one, now study it thoroughly, What Data you are getting? Yes the inside dimensions of the room that is 15m X 6m, This thickness of the wall which will act as the bearing of the beam are 250mm thick, and the Centre to Centre distance between the beam that is 3m.
 
Beam Layout
STEEL BEAM PLAN
 

 

Step 2 – Calculation of the Influence Area of the Structural Steel Beam :-

The Influence Area of a Beam means the area of which the loads are acting that beam, or simply you can say that the beams have to be designed for the loads on that area that is the influence are. Here in this particular problem we see that all the beams are in a similar situation, that means they are within a same room and same direction, they are supporting the same roof with same finishing, and these beams are spaced at a same distance, that means the condition of all these beams are identical to each other, so we will do structural design for any one of the beams and that design will be fit for other beams. If the conditions were not identical then we have to design each of them individually for economy or we have to design the beam which is having the greatest load on it. Let us consider the Beam B for Design
Here all beams are 3m apart C/C distance from each other, hence a single beam B is having Beam A on the left at 3m distance apart and Beam C on the right side is also 3m apart, so the Beam B is supporting half of the load of the area between Beam B and Beam A on the left side and on the right side the Beam B is supporting half of the load of the area between Beam B and Beam C. Hence it means on the left side supporting a strip of (3/2) = 1.5m width and on the right side again supporting a strip of (3/2) = 1.5m width. So the influence area becomes a strip of width 1.5m + 1.5 m = 3m and its length being from centre to centre of the bearing at the each end of the Beam that is the Effective Length of the Beam.

 

Steel Beam, I Section
STEEL BEAM I – SECTION
 

 

Step 3 – Calculation Of Loads acting on the Steel Beam :-

Now we have to calculate the loads acting on that influence area as calculated above as Civil Engineering Structural Design will be based on these Loads. These loads can be broadly classified as Dead Loads and Live Loads. Dad loads means the loads coming from all unmovable Objects like Slab, Beam itself, Flooring etc. and Live Loads Means the load coming due to the movable objects such as we humans, furniture and other movable loads. Generally Dead Loads are calculated and Live Loads are specified according to the Type of the structure, varying in intensities with different types. Like for residential building generally it is 2 KN/ m2 and for Commercial Building it is 4 KN/m2. The Dead Loads which are to be calculated are as follows:-
Dead Loads –  1) Self weight of beam(Assumed 1KN per m)
2) Load of slab supported @25 KN /m3 for R.C.C.
3) Load of floor finishing (generally 0.5KN/m2)
4) Load of Brickwork if any @19.2 KN/m3
All the loads are to be calculated on per m run basis so that it becomes a U.D.L. The total load acting on the beam will be  the sum of the Dead Loads and Live Loads
Therefore, Total Load per metre run, w = Dead Loads + Live Loads
Here in this case the load calculation will be as follows : 

 

A) Dead Loads –

                                I.            Due to the self weight of the beam – 1 KN/m
                              II.            Due to the 150mm thick slab = (1 x 3 x 0.15) x 25 = 11.25 KN/m                                       that is [Length x Breadth x Thickness] x Density
                            III.            Due to Floor Finishing @ 0.5 KN/m2 = (1 x 3) x 0.5 = 1.5 KN/m                                   that is [Length x Breadth] x Load Intensity  
B)Live Load – @ 4 KN/m2 = (1 x 3) x 4 = 12 KN/m  [Length x Breadth] x Load Intensity
Therefore, Total Load per metre run, w = (1 + 11.25 + 1.5) +12 = 13.75 + 12 = 25.75 KN/m
 

Step 4 – Calculation of Effective Length Steel Beam :-

It is taken as the length between the centre of bearings of the beam at each end.
Therefore in our case having a clear span of 6m and 250mm support at each end by means of wall we get,
Effective length, l = 6 + (0.25/2) + (0.25/2) = 6+0.125+0.125 = 6.25m
 

 

Step 5 – Calculation of Maximum Bending Moment On The Steel Beam :-

Here we will introduce the Structural Steel Beam Design Formulae for the first time. Now calculate the maximum bending moment acting on the beam by adopting suitable formula which are as follows :-
i)                    For point load at the mid span of the beam: –  M = (w.l/4)
ii)                  For U.D.L. Throughout the span of the beam :- M= (w.l2/8)
iii)                For Point load at any point of beam :-  M = (w.a.b/l)
For any unusual loading you have to calculate the maximum bending moment and shear force by shear force bending moment diagram drawing procedure.
Here in this case as we are having a U.D.L. of 25.75 KN/m throughout the span hence we will use the second formula that is M = (w.l2/8)
Therefore, in our problem we get,
Maximum Bending Moment, M = (w.l2/8) = ((25.75 x 6.252)/8) = 125.73 KN-m
= 125.73 x1000 x 1000 N-mm = 125730000 N-mm

 

Step 6 – Calculation of Section Modulus Required For Steel I Beam :-

Here we will use another Civil and Structural Engineering Design Formula  for steel beam design. Here we will determine the Section Modulus required in order to resist the Maximum Bending Moment acting on the beam. At the star of this article we had found that (M/I) = (f/y) or (M/f) = (i/y) again Z=(i/ymax) therefore we can rewrite it as Z=(M/f). The value of ‘f’ depends upon the grade of steel and factor of safety. Considering Fe250 Grade of steel, and according to code of practice of the different country the factor safety will vary for obtaining the permissible stress (f) from the Yield Strength of Steel. Here I will follow the IS 800 Code and according to it Maximum Permissible Stress = 0.66 X Yield Strength. But in case of I beam and channel with equal flanges the permissible bending compressive stress shall be calculated from the table given in the code by knowing the value of ((D/T)/(l/ryy)) where,
D = Overall depth of the beam
T = Mean thickness of gthe compression flange, which equals to the area of horizontal portion of flange divided by width
l = Effective length of compression flange
ryy = Radius of gyration of section about its axis of minimum strength (y-y axis)
However the value of permissible compressive stress shall never exceed 0.66fy, where fy = Yield Strength of Steel. Here for easy understanding considering that the permissible compressive stress has got the same value that of 0.66fy.
in case of Fe250 the Yield Strength is 250 N/mm2, Hence Maximum Permissible Stress, f = 0.66 x 250 = 165 N/mm2.
Thus returning to our problem we get that,
Zrequired = (M/f) = (125730000/165) = 762000 mm3       [Unit Derivation,  Z = (i/ymax) = (mm4/mm) = mm3]
For  selecting a suitable section from the steel table that is the chart of Rolled Steel Section we have to get the value in terms of cm3, Hence 762000 mm3 = (762000/(10x10x10)) = 762 cm3
 

 

 

 

Step 7 – Steel I Beam Selection of Suitable Section from Steel Table :-

Now we have to use the steel table which has the standard Rolled Steel Section List and their properties written on. These Tables are country specific and will vary from United Kingdom to United States to Australia to India. So you need to use your country specific steel table. We have to choose a section, preferably a I Section from the Steel Table, which will have a Section Modulus (use section modulus about –x-x axis)  or ‘Z’ equal to or greater than what is found to be required (Zrequired), and also have to note all necessary properties of that Steel Section. In our case I will use SP-6 Steel Table, and I have found the following section to be suitable in case of our Civil Engineering Design Problem:-
Let us Try ISMB 350 @52.4 kg/m Having the following properties,
Sectional Area, a =66.71 cm2
Depth of Section, h = 350mm
Thickness of Web, tw = 8.1mm
Moment of Inertia, Ixx = 13630.3cm4
Section Modulus, Zxx = 778.9 cm3

 

Step 8 – Check For Shear Of Steel Beam :-

As of now we have made a design based on flexural strength that is based on Maximum Bending Moment, and selected such a section which will be safe in Bending. Now we have to check if that section will be safe in shear or not. For this we have to calculate the Maximum Shear Force acting on the beam, as for U.D.L. this can be calculated by using the Structural Engineering Analysis Formula V=(w.l/2) , where,
V = Maximum Shear Force
w = Load per metre run
l = Effective Length of the Beam
Then by this shear force we have to calculate the average shear stress on the beam due to the Maximum Shear Force, by using the formula Tva = (V/h.tw), After getting this Average Shear Stress we have to calculate the permissible Shear Stress which depends upon the grade of steel and also upon the factor of safety which is varying according to Code of Practice of different country, according to IS 800 Permissible Shear Stress = 0.4 x Yield Strength of Steel, Hence for Fe250 Grade Steel we get, Permissible Shear Stress, Tvm = 0.4 x 250 = 100 N/mm2. Now if the permissible stress is greater than or equal to that of the Average Shear Stress on Beam then the Section is Safe In Shear, or else it is unsafe therefore, we have to select the next higher section in terms of Section Modulus and area of Web (h.tw) and give trial for shear check, until it becomes safe.
In Our case of problem it will be as follows :-
Maximum Shear Force, V = (w.l/2) = ((25.75 x 6.25)/2) = 80.45 KN = 80450 N
Average Shear Stress in Beam, Tva = (V/h.tw) = (80450/(350 x 8.1)) = 28.38 N/mm2 < 100 N/mm2
Hence the section is Safe In Shear.
Steel Column Beam Connenction
STEEL COLUMN BEAM CONNECTION

 

Step 9 – Check for Deflection Of Steel Beam :-

We are almost done in the Design of Steel Beam, this the last check we have to perform, the rule is same, if the section satisfies the check then it is safe, or otherwise we have to check with another section having more depth (h). For this check we have to calculate the Actual Deflection on the beam by using the Structural Analysis Formula in case of U.D.L. the formula is  :-
Del(Symbolic) = (5/384) x (W.l3/E.I)
Where,
Del = Deflection in cm
W = Total Load = w.l in N
E = Modulus of Elasticity, For Steel E = 2 x 105 N/cm2
l = Effective Length in cm         [ Small L]
I = Moment of Inertia in cm4   [Notation = Capital Eye]
And Permissible Deflection = l/300
Here, In the case of our problem the calculations will be as follows :-
W = Total Load = w.l = 25.75 x 6.25 = 160.94 KN = 160940 N
E = 2 x 107 N/cm2
l = 6.25 m = 625 cm
I = 13630.3 cm4
Actual Deflection, Del = (5/384) x (W.l3/E.I) = (5/384) X ((160940 X 6253)/((2×107) X 13630.3)) = 1.877 cm
Permissible Deflection = l/300 = 625/300 = 2.083 cm > Actual Deflection, Hence Safe.
Therefore The Section selected by us is Safe in All Respects.
Therefore Let Us Provide ISMB 350 @ 52.4 kg/m

 

Apart from these checks there are also other checks like, Check for Vertical Buckling [Important for Point Loads], Check for Direct Compression in Web, Check for Diagonal Buckling.This check procedure have not been included in this article now, but will be Updated Soon.
For making this Article Universal I’ve used only Common Terms and Denotations which are well known in all of the Countries Like United Kingdom, United States, Australia, India and other places, as the Denotations may vary Code to Code of Different Countries.

 
Now the Structural Design of Steel Beam has successfully completed in all respect. I hope You understood all along with ease, I’ve made it as much as easy as possible. Do Share the Link of this Article On Your Network Of People of All Fellow Civil Engineers and Your Social Network as a Token for Appreciation of this Article if this Article Helped You in Understanding.Keep Visiting MyCivil- Civil Engineering Redefined for more Articles at www.mycivil.engineer. Please do comment on this post, as your comments are very important to me so that I can understand if you are having any problem, and also it will be helpful for others who will visit this Blog. Join This Blog for Regular Updates and also you can now follow us in the Facebook, Twitter and also on LinkedIN. 
 

If you like this Article then I am sure you will like the following well researched articles too, come on check them out also

Concrete Mix Design Step by Step Guide with Example
Top 5 Mistakes at Site You are Doing causing Failure of Concrete
Design of RCC Column in Limit State Method under 5 Minutes
Septic Tank Design for Any Building – Fastest Method
How to Choose Different Foundations Based on Site Conditions

Come Connect with me On Social Media

LinkedIN
Facebook Fan Page
Twitter
Quora
Design Of Steel Beam Fastest Method With Example

Prestressed Concrete Structures A Brief Description With Example

by | Sep 22, 2014 | Structural Analysis

Prestressed Concrete Structure is the one of the most advancement in the Civil Engineering Construction Field, particularly in the Concreting Operation. In the modern day every heavily loaded structures such as Bridges, Flyovers, Railway Sleepers in all these structure where loads are so heavy that Normal RCC will not be enough there prestressed concrete is used. In this article I will share with you the main concept that is the backbone of the Prestressing technique and procedure for the Industrial manufacturing of Prestressed concrete, also after reading this article thoroughly you will understand why one should resort to Prestressed concrete, Advantages of Prestressed concrete over the normal RCC structure. First of all let us understand what the science is being the backbone of this prestressed concrete structures.

 
Prestressed Concrete Working Principle
PRE STRESSING ACTION TO COUNTERACT THE TENSILE STRESSES
 

Why Prestressed Concrete Structures becomes necessary ==>

As you and me already know that a structure under the action of different loads acting on it, the structure takes the shape of bending. The loads acting on a structure causes it to bend in between the supports with shape having convexity downwards that is what we called as positive bending,  and near the support the bending occurs in a reverse shape , that is the convexity is on a upward direction, this we called as the negative bending of the structure. Now due the nature of this kind of bending of the structure the one side of the structure about the Neutral Axis of the section the particles there goes on squeezing that is compressing, and the other side of the Neutral Axis the particles tries to go away from each other, hence tension between the each particles develops. Now the main problem arises because concrete is strong enough t withstand the compressive stresses but it cannot withstand the tensile stresses to a reasonable amount, hence we provided reinforcements to take up this tension.

But what if the loads are very high, I really mean very very high, as in the case of Bridges, Railways Sleepers? will it be able to withstand that high super high amount of tensile stresses?
Yes it can, but the sections will be huge and hence this will not be practical to construct normal RCC on these cases. Apart from this fact any RCC structure will defiantly have cracks (micro cracks) which may not be a matter of concern in case of normal structure, but in case of heavily loaded structure this cracks are not to be allowed, especially in case of water retaining structures. Due to all of these reasons we need to use Prestressed concrete structure.
If we study a Concrete structure we will notice that it is susceptible to failure mainly due to the Tensile stresses. Hence if we can make any arrangements by which there will be no Tensile stresses in the structure or a very little amount of tensile stress which is manageable then we can definitely the solve the problem, But How?
The main concept is that when a structure is loaded it results in bending and thus both the tensile and compressive stress develops now  as the Tensile and Compressive are of two exactly opposite nature of stress so we have to make arrangements to counteract this Tensile stresses, and I know you have guessed it right, Yes we will introduce Compressive Stress in the Tensile zone of the structure with atleast equal amount of that of the tensile stress, so this Compressive stress will counteract and omit the tensile stresses completely and in the whole section there will be no tensile stress and the whole section will become a compressive section. I know, you now know the conclusion don’t you? Yes now as the whole section becomes compressive therefore there is no risks of tensile failure, and about the compressive stress the concrete itself can handle it like captain America.
 

But Wait, How Can We Introduce Fully Compressive Sections? ==>

Simple, we can do this by Prestressing the section. So how to do so is what you want know now. For making prestressed concrete we have to use High Strength concrete made of OPC 53 grade, as the stresses are really high in section due to prestressing it is a must to use High Strength concrete of High Grade, otherwise the section will fail in high compressive stresses. Prestressing is done by means of inserting High Tensile Steel Tendons (similar to cable) in a bunch or in other form inside the section throughout its length about its periphery and exiting from the each end. This tendons are stressed within their Elastic Limit by pulling them at both ends of the structure under the action of machine., then from the both the ends of the structure at the exit points of the tendons arrangements are made by means of wedge so that the tendons are rigidly locked and if the machine releases the tendons, the tendons cannot slip away from the wedge and becomes fixed. As the tendons are pulled from both the ends, tensile stresses are developed, in the tendons, and after releasing the tendons  it tries to go back to its original normal position from its stretched condition, but due to the locking of the tendons at it both ends of the structure, the tendons cannot go back to its initial position, it tries squeeze itself but cannot, due to this squeezing or compression effect and as it cannot go back for being locked with the structure, it is always squeezing the structure along with itself, and hence the compressive stresses develops in that zone on which side Prestressing tendons are provided, and due to loading the amount of tensile stresses developed in that zone is counteracted by the compressive stress developed in the structure due to the prestressing. And thus the whole structure becomes compressive and no tensile stresses are remaining in the structure.

I hope this article helped you in understanding the Prestressed Concrete Structure concept. On the next article I will discuss about How the Prestressed concrete structures are manufactured and Advantages of the Prestressed concrete over RCC and link it to this post. For more Civil Engineering Info, Facts, Technological discussion keep visiting MyCivil – Civil Engineering Redefined. And do share this page in your circles on social network, make this blog large, as you know people like you are the only asset to this blog. Feel free to comment on this post, any comments will be highly appreciated.

If you like this Article then I am sure you will like the following well researched articles too, come on check them out also

Concrete Mix Design Step by Step Guide with Example
Top 5 Mistakes at Site You are Doing causing Failure of Concrete
Design of RCC Column in Limit State Method under 5 Minutes
Septic Tank Design for Any Building – Fastest Method
How to Choose Different Foundations Based on Site Conditions

Come Connect with me On Social Media

LinkedIN
Facebook Fan Page
Twitter
Quora
Design Of Steel Beam Fastest Method With Example

Design Of Columns In Limit State Method with Building Example

by | Oct 29, 2013 | R.C.C. Design

Among the all structural Members the Design of Columns are very important yet the Design of Columns are much neglected. This importance of Structural nature of column is because if any other structural member say Beams or Slabs fails, it will cause only a local failure in that particular portion of the structure.
Whereas, failure of a column means that the of that particular column which has failed will have to be borne by the adjacent columns,hence it will give loads on the adjacent columns beyond their Design Limit. As due to this fact it may start a chain reaction of failures in columns and subsequently the whole structure may collapse. As in the Framed Structured Building that is in the modern day construction the Frames are formed by networks of Columns and Beams. Due to all this reason only even if vertical or Gravity loadings are considered the Design of Columns stands to be of much importance than any other structural Members.
 
A Column is a Structural Member which is vertical and axially loaded and subjected to Compressive forces, and having it’s Effective Length (Height) Three times greater than the least cross-sectional dimension of it self. To Satisfactorily Complete the  Design of Columns The Following Steps must followed.

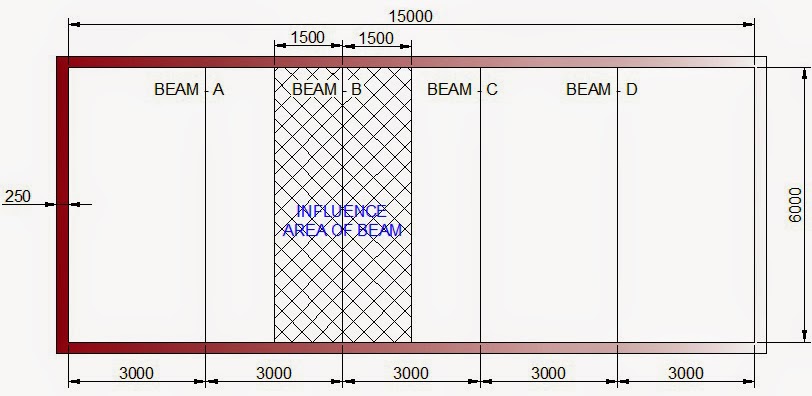
STEP 1 :- Calculation of the Influence Area for Design of Columns :

The first step is to find out the Influence Area of the Column to be Designed. The Influence Area of a column is the area of which load is being transferred to the column to be designed for. For this purpose in a framed structure small and medium building the design of column is done for the column whose Influence Area is the largest hence the load coming on the column will be so the greater of the any other column in that building hence all the other column having lesser Influence Area hence lesser Loads if provided with the same Designed parameters that required for the column having largest Influence Area, then the whole Structure will automatically become safe against the Loads.
 
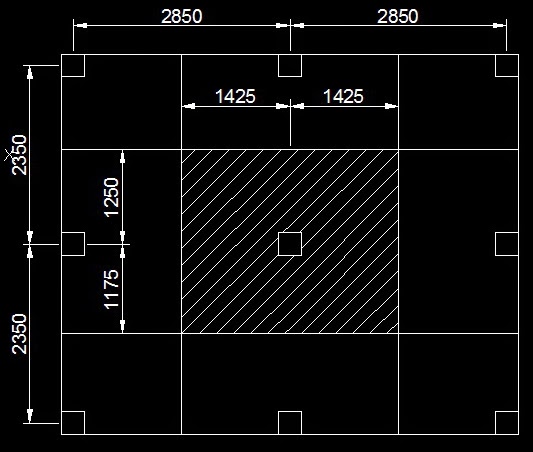Design of Columns Influence Area
DETERMINATION OF INFLUENCE AREAS FOR LOAD DISTRIBUTION ON COLUMNS
 

STEP 2:- Calculation of the Loads Coming on Columns from the Influence Area :

In this step the Load Calculation is being done. This is done by calculating all the loads acting within the influence area.
The Loads acting are broadly classified as Dead Load (DL) and Live Load (LL). Dead Loads are the load of objects which cannot be moved from on place to another like the loads of Brick Work, Beams, Slabs etc. and the Live Loads are the loads coming from movable objects such as Humans, Chair, Table etc.
Thus We Need to Calculate the Dead Loads as well as Live Loads within the Influence Area, these are as follows in the general case of a Building :-
 
A)Dead Loads :
        I.            Due to weight of Slab                                    [25000 N/m3 ]
      II.            Due to weight of Floor Finish                        [500 N/m2]
    III.            Due to weight of Brick Masonry                   [19200 N/m3]
    IV.            Due to weight of Beam                                 [25000 N/m3]
      V.            Due to weight of Self Weight of Column        [25000 N/m3]
 
 
B) Live Load :

It depends upon the Nature of the Structure, and it values for different structural nature are given in the concerned Code of Practice, like in India these are given in I.S.: 875-Part II.

For Residential Buildings it is generally considered @ 2KN/m2 = 2000 N/m2
 
Column Shuttering Design of Columns
COLUMN FORM WORK OF BUILDING

Now after correct calculation of above loads the Total Load is Calculated by,

Total Load on each floor = Dead Load + Live Load
Now this the actual load which will be acting on column for each floor, now if the building say 5 storied, then just multiply the value with the nos. of floors, like for five storied building multiply the Total Load on each story with 5.
Now thus the Total load acting on column at Column Base is Obtained and it is denoted with ‘P’.
Hence P= Total Load on each Floor X Nos. of Stories = (Dead Load + Live Load) X Nos. of Stories.
Now we shall move to the actual Designing to determine suitable Column sections and its Reinforcements so that the above load is safely resisted by the column Designed.
It can be done by Three main Methods of Design : a) Working Stress Method b) Ultimate Load Method and c) Limit State Method.
The Modern Practice is to use Limit State Method for all types of Designing, Hence I’ll discuss here the Limit State Method Of Design Of Columns.

STEP 3 :-Finding The Gross Cross-Sectional Area Required For The Design of Columns :

This is the one of the most important and main step of the Design of Columns.
First in the Limit State Method of Design of Columns we must increase the load acting on the column with a Load Factor so that if there will be any accidental increase of loads the column will be still safe to resist the load without a failure. The Factor of Safety for Dead Load + Live Load Combination is 1.5, hence we must multiply the load action on column (P) with the 1.5 to obtain the Ultimate Load that is the Factored Load of the Column that is Pu.
Hence Factored Load, Pu = 1.5 X P
For Design we will work with this value of load.
Now before going on I’m here to say that I will design according to the Code Of Practice of I.S.: 456-2000
The Ultimate Load of a Column is given by,
 
Pu = 0.4.fck.Ac + 0.67.fy.Asc   [Equation I]
Where, Pu = Ultimate Load of the Column in N/mm2
              fck= Yield Strength of Concrete in N/mm2
              Ac = Area of Concrete (Cross-Sectional Area) of Column in mm2
               fy = Yield Strength Of Steel in N/mm2
            Asc= Area of Steel (Cross-Sectional Area) in Column in mm2
 
Now the column consists of Concrete and as well as Steel in the form of Reinforcements hence the Total Cross-Sectional Area of Column is made of Area of Concrete and Area of Steel.
 
The Total Cross-Sectional area of Column can be also termed as Gross Cross-Sectional Area of Column and it’s denoted by Ag.
Hence, Gross Cross-Sectional Area of Column = C/S  Area of Concrete + C/S Area of Steel
Therefore, Ag = Ac + Asc
And hence, Ac = Ag – Asc
 
Now putting the above obtained value in the original equation (Equation I) we get,
Pu = 0.4.fck.(Ag-Asc) + 0.67.fy.Asc  [Equation II]
Now Assume the Percentage of Steel you want to use ranging anywhere from 0.8% to 6% with Respect to Gross Cross-Sectional Area of the Column (Ag). Say Assuming Steel as 1% of Ag it means Area of Steel Asc = 1% of Ag = 0.01Ag
 
The higher will be the percentage of steel used the lower will be Ag and thus lesser will be the cross-sectional dimension of the column. But the as the Price of Steel is very high as compared to the Concrete hence it is desirable to use as less as steel possible to make the structure economical, again if the percentage of steel is lowered then the Ag will increase at higher rate, about 30% with decrease of just 1% of steel and so each lateral dimension of the column will increase and will cause a gigantic section to be provided to resist the load. Therefore both the factors are to be considered depending upon the amount of loading.
 
My suggestion is to use the following Percentage of steel for the Design of Column, Which I’ve found to be effective and to produce economical and safe section of Column.
 
 

Loading (Pu) in N             Percentage Of Steel  for Satisfactory Design

Below 250000 ——————————————–0.8%
250,000 to 500,000 ————————————–1.0%
500,000 to 750,000 ————————————–1.5%
750,000 to 1000,000 ————————————-2.0%
1000,000 to 1500,000 ———————————–2.5%
1500,000 to 2000,000 ———————————–3.0%
 
And so on, with increase of each 250,000 N increasing the Percentage of Steel as 0.5%.
 
Now  input the value of the Asc in the form of Ag in the Equation I. For example suppose 1% Steel is used then the equation will be like the one below :-
Pu = 0.4.fck.(Ag-0.01Ag) + 0.67.fy.0.01Ag
 
Therefore, if we know the Grade of Concrete and Grade of Steel to be used and Factored Load coming on the Column and Assuming the Percentage of steel required appropriately then we can Very Easily Calculate the Gross-Sectional Area (Ag) of the Column required from the above form of the equation.
Now as the Ag is obtained thus the Lateral Dimensions of the Column that are the sides of the column can be easily determined.
 
The Ag or Gross-Sectional Area of the Column means that it is the product of the two lateral sides of a column [i.e. Breadth (b) X Depth (D)], hence reversely knowing the Ag we can determine the Lateral Dimensions.
For making a Square Section just Determine the Root Value of the Ag. Like if the Value of Ag is 62500 mm2Then considering square section of a column we can get each side
Square Column Section Design of Columns
Also Rectangular Column Sections Can be made by using different proportion say b : D = 1 : 2 , Hence D=2b , Therefore, Ag = b X D = b X 2b = 2b2 or b=
 
Gross-Sectional Area Of Design of Columns
Hence D can be also determined as D=2b after Calculating the b.
Most of the times after calculating the sides of a column it will give results such as 196.51mm or 323.62 etc. values, which practically cannot be provided at field, hence we must increase those values to the nearest greater multiple of 25mm (i.e. 1 inch). For examples a value of 196.51mm may be increased to 200mm or 225mm or 250 mm even, and a value of 323.62mm may be increased to 350mm. more it will be increased the more it will be safer, but it is uneconomical to increase by a very high amount, it should not be increased more than by 75mm to consider the economical factor.

STEP 4 : Check For Long/Short Columns:

 
Depending upon the ratio of Effective Length to the Least Lateral Dimension of a column, a column may be classified as Long Column and Short Column. If the value of this ratio is less than 12 then it’s called as a short column and if the value is more than 12 then it’s called as a Long Column. A short column mainly fails by direct compression and has a lesser chance of failure by buckling. And in the case of a long column the failure mainly occurs due to the buckling alone. Long column being slender, that is being thin like stick as compared with its length it grows a tendency to get bend by deviating from its vertical axis under the action of loads. Due to this tendency of long column to get buckled (bend) a long column of all same properties and dimensions that of a short column will be able to carry much lesser load safely than that of the short column.
 
Suppose a 400mmx400mm short column can take a load of 1000KN , then a long column of 400mmx400mm having same grade of concrete, same amount of reinforcement and same workmanship will be able to carry a lesser load like say about 800KN only, hence we get a loss of 200KN which is 20% loss of load carrying capacity. So the above formula used in Step 3 holds good only for the Short Column. For using it in long column a little modification is needed, which I will update it later when I will get hands on this article again. For now let us concentrate on Short Column. First of all we need to find out the effective length of a column, which can be obtained by multiplying a factor with the actual unsupported length of the column. The factor depends upon the end condition of the column. In most general cases we use a Both End Fixed Column for which The Factor is 0.65.
 
Therefore, Effective Length = Effective Length Factor (0.65) x Unsupported Length (l). suppose a column has a unsupported length of 2.7m = 2700mm, hence the effective length will be lef = 0.65×2700 = 1755mm. Least lateral dimension means the shorter of the two dimensions of column that is length and breadth. But in case of a circular column as there is only diameter, hence we will use the diameter.
 
Suppose a column is of 400mmx200mm section and has an unsupported length of 2700mm, then the Ration of Effective length t the Least Lateral Dimension will be as follows :-
(Effective Length/Least Lateral Dimension) = (lef/b) = (1755/200) = 8.775 which is less than 12 and hence is a Short Column.
 

STEP 5  Check For Eccentricity for Design of Columns :

Eccentricity means deviating from the true axis. Thus an Eccentric Load refers to a load which is not acting through the line of the axis of the column in case of column design. The eccentric load cause the column to bend towards the eccentricity of the loading and hence generates a bending moment in the column. In case of eccentric loading we have to design the column for both the Direct Compression and also for the bending moment also. Practically all columns are eccentric to some extent which may vary from few millimetres to few centimetres. In practical field it is almost impossible to make a perfectly axially loaded column, as a reason we have to consider a certain value of eccentricity for safety even though if we are designing for a axially loaded column. The conditions of considering eccentricity and its value may differ from code to code according to the country.
 
Here I will tell you what I.S. : 456-2000 says. According to it the eccentricity which we have to consider for design must be taken as the greater of the followings :-
i) 20mm.
ii) (lef/500) + (b/30)
Where,
lef = Effective Length of the Column
b = Lateral Dimension of the Column (We have to calculate two separate values for two sides in case of rectangular column)
Permissible Eccentricity :- 0.05b where b is the dimension of a side of a column, we have to check for two sides separately in case of rectangular column.

The Permissible eccentricity must be greater than or equal to the actual eccentricity of the column. Or else we have to design it for bending also.

STEP 6 :-Calculating The Area Of Steel Required for Design of Columns :

Now the Area of Steel Required Asc is to be calculated from the Ag as the predetermined percentage of Ag. For example if the Gross-Sectional Area of the Column is 78600 mm2and at the starting of calculation of Ag it was assumed that 1% Steel is used then we get,
Asc = 1% of Ag = 0.01Ag = 0.01 X 78600 = 786 mm2
Now we shall provide such amount of Reinforcements that the Cross-Sectional Area of the Reinforcement provided is Equal to or Greater than the Cross-Sectional Area of Steel required above.
Hence in the above case we shall Provide 4 Nos. of 16mm Diameter Bars
Hence, The Actual Area of Steel Provided,
Area Of Steel In Column
Hence the Area of Steel Provided is Greater than Area Of Steel Required, Hence the Structure will be Safe.
 
NOTE : The minimum of 4 Nos. of Bars to be provided at the four corners of a rectangular or Square Columns and minimum diameter of Bars that to be used is 12mm Diameter. Hence 4 Nos. of 12mm Diameter Bars are must in any Columns irrespective of their necessities.
 

STEP 7 :-Determining The Diameter and Spacing Of The Lateral Ties for Design of Columns:

In this step we will Determine the Diameter and the Spacing of the Lateral Ties or Transverse Links or Binders.
 
The Diameter of the Ties shall not be lesser than the Greatest of the following two values 

  1.  6mm 
  2.  1/4th of the Diameter of the Largest Diameter Bar
 
For an example if a Column has 16mm and 20mm both types of bar as Longitudinal Bars or main Reinforcement then 1/4th of 20mm = 5mm Hence we shall provide 6mm diameter Ties.
 
The Spacing of Ties shall not exceed the least of the followings three values 

  1.  Least Lateral Dimension 
  2. 16 Times of the Diameter of the Smallest Diameter Longitudinal Bar 
  3. 48 Times of the Diameter of Ties
 
For an example A Column of 250mm X 350mm Dimension having 20mm and 16mm Diameter Longitudinal Bars and 6mm Diameter Ties we get,

  • Least Lateral Dimension = 250mm 
  • 16 Times of the Diameter of the Smallest Diameter Longitudinal Bar = 16 X 16 = 256mm 
  • 48 Times of the Diameter of Ties = 48 X 6 = 288mm
Hence Provide 5mm Diameter Ties @ 250mm C/C                                                                       

[In this case our objective is to minimize the value to reduce the spacing and to make the structure more stable, hence we shall take least value and suitably in a multiple of 25mm]

 

If you like this Article then I am sure you will like the following well researched articles too, come on check them out also

Concrete Mix Design Step by Step Guide with Example
Top 5 Mistakes at Site You are Doing causing Failure of Concrete
Design of RCC Column in Limit State Method under 5 Minutes
Septic Tank Design for Any Building – Fastest Method
How to Choose Different Foundations Based on Site Conditions

Come Connect with me On Social Media

LinkedIN
Facebook Fan Page
Twitter
Quora
Design Of Steel Beam Fastest Method With Example

Reinforced Concrete Advantages Over Plain Concrete

by | Oct 14, 2013 | R.C.C. Design

R.C.C. stands for Reinforced Cement Concrete, and now a days is the main Constructional Material which is used to construct different structural parts, by using R.C.C. it has been made possible to construct High Rise Buildings which were formerly only constructed with Pure Steel Structure but by using R.C.C. in the modern age it has now become an easy and economical approach to attain such high strength to withstand such tremendous imposing loads on structure.
R.C.C. is actually consisting of two main different parts firstly Concrete and secondly Reinforcement in the form of Steel. As we all know that when ever loads come on a structure it tries to take the shape of bending, and the nature of bending depends upon it’s supports and their respective positions. When the shape of bending takes a shape convexity downward then it’s called as Sagging and the Bending the an corresponding Bending Moment is Treated as +ve , and when the shape of the bending takes a shape of convexity upwards then it’s called as Hogging and the Bending and corresponding Bending Moment is treated as –ve.

Why Reinforcement is Needed?

Due to the bending of a structure one side of the structure about Neutral Axis Compresses and the other side is tensed, due to the above fact Compressive Stress and Tensile Stress develops in the structure from the Neutral Axis towards the Extreme Fiber that is the exterior face of the structure in a increasing manner in terms of magnitude of the stresses. So the Structure is having both Compressive and Tensile Stresses in it.
In the case of a Concrete, it has enough resistance against Compressive Stresses but it is very very Weak in Tensile Stresses and it can only resist a very little Tensile Stress which is as good as negligible. Hence to make a structure safe and in working condition to take up the Design Loads the structural material must e able to withstand both Tensile as well as Compressive Stresses, now as the Concrete is not strong to withstand the Tensile stress, so some measures is to be taken and it is to be provided with something which will take up the Tensile Stresses developed in Concrete. Due to the above fact A Structural Member such as Column, Beam, Slab etc are not made of Plain Concrete, instead it’s Reinforced with Steel embedded in it, which take ups the Tensile Stresses developed.

Why Steel is Used As Reinforcement?

Due to the change of temperature the Concrete Expands and Contracts, and the material used for Reinforcing will also expand and contract due to the change of temperature, depending upon their Co-efficient of Volumetric Expansion. If the change of Volume of Concrete and embedded Reinforcement will not be of same amount the at the surface of contact between Concrete and Reinforcement Differential Stresses will develop hence crack will develop and will cause failure of the structure. It is experimentally found that the Co-efficient of Expansion of Concrete and Steel is almost same, hence due to the change of temperature No Differential Stresses will Develop, hence No Cracks, and No Failure, this is the main reason why steel is used as Reinforcement.

Follow MyCivil at :-

Shear Force And Bending Moment Diagram For Simply Supported Beam

Shear Force And Bending Moment Diagram For Simply Supported Beam

by | Mar 27, 2013 | Structural Engineering

Simply Supported Beam With Point Load At It's Mid Span

Here Below the Step by Step Procedure to draw Shear Force and Bending Moment Diagram of a Simply Supported Beam with a Point Load at Mid Span is Given :
Step 1 :- Calculation Of Reaction ==>

∑V=0
Therefore,
RA + RB – W = 0 or RA + RB = W or RA + RB = 10KN …….(i)
∑MB=0
Therefore,
+(RA*5) –(10*2.5) +(RB*0) = 0   or   +(RA*5) –(10*2.5) = 0  or  (RA*5) = (10*2.5) or RA = (10*2.5)/5
or RA = 25/5  or RA=5KN
Now putting the Value of RA in the equation(i) we get,
5 + RB = 10 or RB = 10-5 or RB=5KN
Therefore, RA=5 KN  and  RB=5KN


Step 2 :- Shear Force Calculation ==>

Shear Force at Point A(L) = 0KN

Shear Force at Point A(R) = 0+5 = 5KN
Shear Force at Point C(L) = 5KN
Shear Force at Point C(R) = 5-10 = -5KN
Shear Force at Point B(L) = -5KN
Shear Force at Point B(R) = -5+5 = 0KN
Step 3 :- Bending Moment Calculation ==>
Bending Moment about Point A = 0KN-m
Bending Moment about Point B = +(5*2.5) = 12.5KN-m
Bending Moment about Point A = +(5*5) –(10*2.5) = 25-25 = 0KN-m

Now Plot these Value in Paper in for making the required Diagram, to some suitable scale. It will look like the Below One.

Shear Force And Bending Moment Diagram

Fill up the Diagram area with Hatch, I couldn’t give it due to Photoshop Problem.

For Details Of Reaction Calculation Concept Go To Link Below
Reaction Calculation Guide For Simply Supported Beam with Point Load

Follow Techno Genome at :-

Support Reaction Calculation Guide For Simply supported Beam

Support Reaction Calculation Guide For Simply supported Beam

by | Mar 27, 2013 | Structural Engineering

Simply Supported Beam With Point Load
Here I will discuss about step by step Support Reaction Calculation Procedure. Say, there is a Simply Supported Beam with a Span Length Of L and Having a Point Load W at the Mid Span of the Beam. There are two supports A & B. The Reaction of Support A is RA and the Reaction of Support B is RB.
Now, The whole lode is to be carried by the two supports, as the beam is symmetrical and carrying the point load at the mid span it is thus obvious the total load will be equally shared between two supports. So the The Support A will take Half of the Load ( i.e. W/2) and the Support B will also carry Half of the Load ( i.e. W/2). To make the Beam to stay in Equilibrium The Total Load The Beam is Carrying must be equal to The Total Reaction The Supports are Giving.Thus,
RA + RB must be equal to W or RA + RB – W = 0. That means Sum of the Vertical Forces must be Equal to Zero, This the First Condition Of Equilibrium.
Now Calculating the Moments, here the Third Condition of Equilibrium that algebraic Sum of the all Moments about a section must be equal to Zero.
Taking Moment About B. Sign Conventions are, From Left to Right Clockwise Moment is taken as Positive and Anti-Clockwise Moment is taken as Negative.

Now first Observe the Loads and Reactions. There is only a single load in the mid span. That means The Distance of the Point Load and the Support B is Half of the Span i.e. L/2. And there are Two Reactions, RA and RB at two supports. Now Starting from the Support A and going towards support B we find 3 Forces one after another in the following Order, RA, W and RB. Now Calculating the Moment about B :-

+(RA*L) -(W*(L/2)) +(RB*0)= 0

Now as the Distance between the Point B and the Line of Action of the force RB is 0, the moment generated due to the force RB about the Point B is is equal to Zero. Thus the equation becomes,

+(RA*L) -(W*(L/2)) = 0  or  +(RA*L) = (W*(L/2))  or  RA = (W*(L/2))/L.
Thus, we can find the RA, and as the whole load is carried by the the two supports, the value of RB will be,

RB = Total Load – RA or RB = W – RA , or just simply put the value of RA in the first equation,           

RA + RB – W = 0.

The above Procedure is a general procedure to Calculate the Reactions for any type of point Loading on a Simply supported Beam.
In the above case the reaction can be known easily as the Beam is carrying the point load at the mid span. The load sharing will be two equal half of the load on two supports, thus the Reactions will be equal to Half of the load at each of the supports.

Follow Techno Genome at :-