Articles | Bastukar

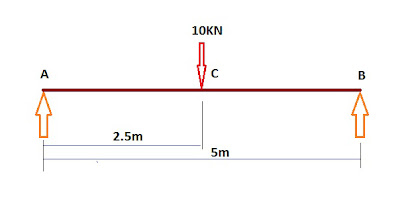
Shear Force And Bending Moment Diagram For Simply Supported Beam

by Bastukar | Mar 27, 2013 | Structural Engineering

Simply Supported Beam With Point Load At It's Mid Span

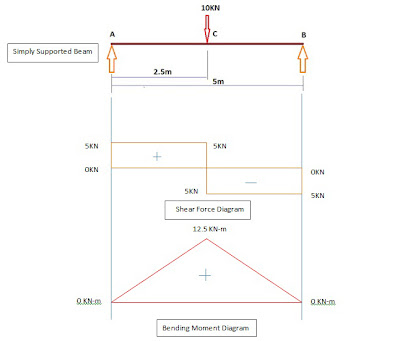
Here Below the Step by Step Procedure to draw Shear Force and Bending Moment Diagram of a Simply Supported Beam with a Point Load at Mid Span is Given :
Step 1 :- Calculation Of Reaction ==>

∑V=0

Therefore,

RA + RB – W = 0 or RA + RB = W or RA + RB = 10KN …….(i)

∑MB=0

Therefore,

+(RA*5) –(10*2.5) +(RB*0) = 0 or +(RA*5) –(10*2.5) = 0 or (RA*5) = (10*2.5) or RA = (10*2.5)/5

or RA = 25/5 or RA=5KN

Now putting the Value of RA in the equation(i) we get,

5 + RB = 10 or RB = 10-5 or RB=5KN

Therefore, RA=5 KN and RB=5KN

Step 2 :- Shear Force Calculation ==>

Shear Force at Point A(L) = 0KN

Shear Force at Point A(R) = 0+5 = 5KN

Shear Force at Point C(L) = 5KN

Shear Force at Point C(R) = 5-10 = -5KN

Shear Force at Point B(L) = -5KN

Shear Force at Point B(R) = -5+5 = 0KN

Step 3 :- Bending Moment Calculation ==>

Bending Moment about Point A = 0KN-m

Bending Moment about Point B = +(5*2.5) = 12.5KN-m

Bending Moment about Point A = +(5*5) –(10*2.5) = 25-25 = 0KN-m

Now Plot these Value in Paper in for making the required Diagram, to some suitable scale. It will look like the Below One.

Fill up the Diagram area with Hatch, I couldn’t give it due to Photoshop Problem.

For Details Of Reaction Calculation Concept Go To Link Below
Reaction Calculation Guide For Simply Supported Beam with Point Load

Follow Techno Genome at :-

Support Reaction Calculation Guide For Simply supported Beam

by Bastukar | Mar 27, 2013 | Structural Engineering

Here I will discuss about step by step Support Reaction Calculation Procedure. Say, there is a Simply Supported Beam with a Span Length Of L and Having a Point Load W at the Mid Span of the Beam. There are two supports A & B. The Reaction of Support A is RA and the Reaction of Support B is RB.

Now, The whole lode is to be carried by the two supports, as the beam is symmetrical and carrying the point load at the mid span it is thus obvious the total load will be equally shared between two supports. So the The Support A will take Half of the Load ( i.e. W/2) and the Support B will also carry Half of the Load ( i.e. W/2). To make the Beam to stay in Equilibrium The Total Load The Beam is Carrying must be equal to The Total Reaction The Supports are Giving.Thus,

RA + RB must be equal to W or RA + RB – W = 0. That means Sum of the Vertical Forces must be Equal to Zero, This the First Condition Of Equilibrium.

Now Calculating the Moments, here the Third Condition of Equilibrium that algebraic Sum of the all Moments about a section must be equal to Zero.

Taking Moment About B. Sign Conventions are, From Left to Right Clockwise Moment is taken as Positive and Anti-Clockwise Moment is taken as Negative.

Now first Observe the Loads and Reactions. There is only a single load in the mid span. That means The Distance of the Point Load and the Support B is Half of the Span i.e. L/2. And there are Two Reactions, RA and RB at two supports. Now Starting from the Support A and going towards support B we find 3 Forces one after another in the following Order, RA, W and RB. Now Calculating the Moment about B :-

+(RA*L) -(W*(L/2)) +(RB*0)= 0

Now as the Distance between the Point B and the Line of Action of the force RB is 0, the moment generated due to the force RB about the Point B is is equal to Zero. Thus the equation becomes,

+(RA*L) -(W*(L/2)) = 0 or +(RA*L) = (W*(L/2)) or RA = (W*(L/2))/L.
Thus, we can find the RA, and as the whole load is carried by the the two supports, the value of RB will be,

RB = Total Load – RA or RB = W – RA , or just simply put the value of RA in the first equation,

RA + RB – W = 0.

The above Procedure is a general procedure to Calculate the Reactions for any type of point Loading on a Simply supported Beam.
In the above case the reaction can be known easily as the Beam is carrying the point load at the mid span. The load sharing will be two equal half of the load on two supports, thus the Reactions will be equal to Half of the load at each of the supports.

Follow Techno Genome at :-

Twitter

Facebook Fan Page

Google Plus

Materials Required For ASF, Plastering & Neat Cement

by Bastukar | Mar 22, 2013 | Construction Practices

Here is how to become a Concrete Calculator by yourself for different types of concrete operation like concrete floor , plaster wall , ceiling plaster, cement finishing etc. works.

1) Artificial Stone Flooring ===>

The Quantity of materials required for 100 Sq.m. 25mm Thick Artificial Stone Flooring 3mm Topping is

Cement @ 0.859 or 25 Bags
Sand @ 0.97 cu.m or 28 Bags
Stone Chips (6mm and Down) @ 1.94 cu.m or 56 Bags

2) Cement and Sand Plastering===>

For 100 Sq.m Of Plastering the required Quantity Of Materials are :

With Cement Mortar (1:6) :-

12mm thick ——– Cement = 0.274 cu.m or 8 Bags Sand = 1.64 cu.m. or 48 Bags

15mm thick ——– Cement = 0.342 cu.m. or 10 Bags Sand = 2.05 cu.m. or 59 Bags

20mm thick ——– Cement = 0.456 cu.m. or 13 Bags Sand = 2.74 cu.m. or 79 Bags

With Cement Mortar (1:4) :-

10mm thick ——– Cement = 0.319 cu.m. or 9 Bags Sand = 1.29 cu.m. or 37 Bags

6mm thick ——— Cement = 0.192 cu.m. or 6 Bags Sand = 0.77 cu.m. 22 Bags

3) Neat Cement Punning===>

Quantity Of Materials Required for 100 Sq.m. Of Neat Cement Punning is as follows:-

1.5mm Thick ——- Cement = 0.186 cu.m. or 5.5 Bags

3mm Thick ——- Cement = 0.375 cu.m. or 11 Bags

6mm Thick ——- Cement = 0.750 cu.m. or 22 Bags

Follow Techno Genome at :-

Twitter

Facebook Fan Page

Google Plus

Quantity Of Materials Required For Brickwork

by Bastukar | Mar 21, 2013 | Construction Practices

The following are the Quantity Of Materials Required for different types of Civil Engineering Works ;-

1) Brickwork in Cement Mortar (1:6) ===>

For 10 cu.m. Of Brickwork in Cement Mortar (1:6) The Consumption Of Materials are

With Modular Bricks :-

Bricks @ 5000 Nos.

Cement @ 0.504 cu.m. or 15 Bags

Sand @ 3.02cu.m. or 87 Bags

With Traditional Bricks :-

Bricks @ 4079 Nos.

Cement @ 0.313 cu.m. or 9 Bags

Sand @ 1.88cu.m. or 54 Bags

2) Brickwork in Cement Mortar (1:4) ===>

With Modular Bricks :-

For 100 Sq.m.100mm thick Brickwork in Cement Mortar (1:4) The Consumption Of Materials are

Bricks @ 5000 Nos.

Cemnent @ 0.63 cu.m. or 19 Bags.

Sand @ 2.52 cu.m. or 73 Bags

With Traditional Bricks :-

For 100 Sq.m.127mm thick Brickwork in Cement Mortar (1:4) The Consumption Of Materials are

Bricks @ 5181 Nos.

Cement @ 0.80 cu.m. or 23 Bags.

Sand @ 3.20 cu.m. or 92 Bags

Follow Techno Genome at :-

Twitter

Facebook Fan Page

Google Plus

Quantity Of Materials Required For Concrete Work

by Bastukar | Mar 21, 2013 | Construction Practices

The Following are the Quantity Of Materials Required for the Concrete Works Of Different Types

1) P.C.C. With Graded Stone Chips :

For 10 cu.m. Of Plane Cement Concrete Work with Graded Stone Chips

For M10 Grade :-

Cement @ 1.54 cu.m or 45 Bags
Sand @ 4.62 cu.m or 133 Bags
Stone Chips @ 9.24 cu.m. or 266 Bags.

For M15 Grade :-

Cement @ 2.2 cu.m or 65 Bags
Sand @ 4.4 cu.m or 127 Bags
Stone Chips @ 8.8 cu.m. or 254 Bags.

For M20 Grade :-

Cement @ 2.8 cu.m or 81 Bags
Sand @ 4.2 cu.m or 121 Bags
Stone Chips @ 8.4 cu.m. or 242 Bags.

For M25 Grade :-

Cement @ 3.85 cu.m or 111 Bags
Sand @ 3.85 cu.m or 111 Bags
Stone Chips @ 7.7 cu.m. or 222 Bags.

2) P.C.C. With Brick Ballast or Brick Chips :

For 10 cu.m. Of Plane Cement Concrete Work with Brick Ballast

For M5 Grade :-

Cement @ 1.00 cu.m or 29 Bags
Sand @ 5.00 cu.m or 144 Bags
Brick Ballast @ 10.00 cu.m. or 288 Bags.

For M7.5 Grade :-

Cement @ 1.18 cu.m or 34 Bags
Sand @ 4.74 cu.m or 137 Bags
Brick Ballast @ 9.48 cu.m. or 273 Bags.

For M10 Grade :-

Cement @ 1.23 cu.m or 36 Bags
Sand @ 4.92 cu.m or 142 Bags
Brick Ballast @ 9.85 cu.m. or 284 Bags.

For M15 Grade :-

Cement @ 2.29 cu.m or 66 Bags
Sand @ 4.57 cu.m or 132 Bags
Brick Ballast @ 9.14 cu.m. or 264 Bags.

3) R.C.C. With Graded Stone Chips :

For 10 cu.m. Of Reinforced Cement Concrete Work with Graded Stone Chips, The Amount Of Cement, Sand, Stone Chips Required are same as that of the P.C.C.

Quantity Of Steel Required :-

For Normal Slab, Chajja, Lintel = 785kg or 0.785 Ton
For Roof Slab = 1180kg or 1.18 Ton
For Stair = 1570kg or 1.57 Ton
For Column and Beams = 1960kg or 1.96 Ton

Quantity Of Binding ( Black Annealed Wire) Wire Required :-

For Normal Slab, Chajja, Lintel = 0.785kg
For Roof Slab = 1.18kg
For Stair = 1.57kg
For Column and Beams = 1.96kg

Follow Techno Genome at :-

Twitter

Facebook Fan Page

Google Plus

Unit Conversions Used In Engineering

by Bastukar | Mar 21, 2013 | Construction Practices

The following are the various important measurements which are required for the day to day work in Civil Engineering :-

Weight Of 1 Bag Of Cement = 50kg
Volume Of 1 Bag Of Cement = 0.0347 cu.m.
Weight Of 1 cu.m. Of Mild Steel = 7850kg
Weight Of Concrete 1 cu.m. Of Plain Cement Concrete = 2400kg
Weight Of Concrete 1 cu.m. Of Reinforced Cement Concrete = 2500kg

Lenear Measurements==>

1m = 100cm
1m = 1000mm
1m = 3.28 ft.
1m = 39.37 inches.
1ft. = 0.305m
1ft. = 12 inches
1ft = 30.48cm
1ft. = 304.8mm
1 inch. = 0.0254m
1 inch. = 0.0833ft.
1 inch = 2.54cm
1 inch. = 25.4mm

Area Measurements===>

1 Sq.m. = 10000 Sq.cm.
1 Sq.m = 1000000 Sq.mm.
1 Sq.m. = 10.76 SFT (Sq.ft.)
1 Sq.m. = 1550 Sq.inches.
1 Sq.ft. = 0.093 Sq.m.
1 Sq.ft. = 0.007 Sq.inches
1 Sq.ft. = 0.155 Sq.cm
1 Sq.ft. = 0.0016 Sq.mm.

Volume Measurements===>

1 Cu.m. = 1 x 10^6 Cu.cm.
1 Cu.m. = 1 x 10^9 Cu.mm.
1 Cu.m. = 35.288 CFT ( Cu.ft.)
1 Cu.m = 61023.28 Cu.inches
1CFT = 0.028 Cu.m.
1CFT = 1728 Cu.inches
1CFT = 0.061 Cu.inches
1CFT = 0.000061 Cu.mm.